SQUID

A SQUID (for superconducting quantum interference device) is a very sensitive magnetometer used to measure extremely weak magnetic fields, based on superconducting loops containing Josephson junctions.

SQUIDs are sensitive enough to measure fields as low as 5 a T (5×10⁻¹⁸ T) within a few days of averaged measurements.^[1] Their noise levels are as low as 3 fT·Hz^-½.^[2] For comparison, a typical refrigerator magnet produces 0.01 tesla (10⁻² T), and some processes in animals produce very small magnetic fields between 10⁻⁹ T and 10⁻⁶ T. Recently invented SERF atomic magnetometers are potentially more sensitive and do not require cryogenic refrigeration but are orders of magnitude larger in size (~1 cm³) and must be operated in a near-zero magnetic field.

1 History and design
- 1.1 DC SQUID
- 1.2 RF SQUID
2 Uses
3 See also
4 References

History and design

There are two main types of SQUID: direct current (DC) and radio frequency (RF). RF SQUIDs can work with only one Josephson junction, which might make them cheaper to produce, but are less sensitive.

DC SQUID

The DC SQUID was invented in 1964 by Robert Jaklevic, John J. Lambe, James Mercereau, and Arnold Silver of Ford Research Labs after Brian David Josephson postulated the Josephson effect in 1962, and the first Josephson Junction was made by John Rowell and Philip Anderson at Bell Labs in 1963. It has two Josephson junctions in parallel in a superconducting loop. It is based on the DC Josephson effect. In the absence of any external magnetic field, the input current $I$ splits into the two branches equally. Now, consider if a small amount of external flux is applied to the superconducting loop. This results in the screening currents that generate the magnetic field to cancel this applied external flux. 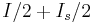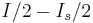The current in one of the branches of the superconducting loop is in the direction of $I$ , and is equal to $I/2 %2B I_s/2$ and in the second branch is in the opposite direction of $I$ and is equal to $I/2 - I_s/2$ . As soon as the current in any one of the branches exceeds the critical current for the Josephson junction, a voltage appears across the junction. Now consider if the external flux is further increased and it now exceeds 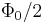$\Phi_0/2$ . Since the flux enclosed by the superconducting loop must be an integral number of the flux quanta, in this case the SQUID instead of screening the flux, energetically prefers to increase it to 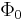$\Phi_0$ . The screening current now flows in the opposite direction. Thus the screening current changes direction every time the flux increases by half integer multiples of 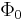$\Phi_0$ . Thus the critical current oscillates as a function of the applied flux. If the input current is more than 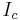$I_c$ , then the SQUID always operates in the resistive mode. The voltage in this case is thus a function of the applied magnetic field and the period equal to 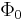$\Phi_0$ . Since the current-voltage characteristics of the DC SQUID is hysteretic, a shunt resistance, $R$ is connected across the junction to eliminate the hysteresis (in the case of copper oxide based high temperature superconductors the junction's own intrinsic resistance is usually sufficient). The screening current is the applied flux divided by the self inductance of the ring. 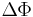Thus $\Delta \Phi$ can be estimated as the function of 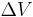$\Delta V$ (flux to voltage converter)^[3]^[4]^[5] as follows:

∆V = R ∆I

2I = 2 ∆Φ/L, where L is the self inductance of the superconducting ring

∆V = (R/L) ∆Φ

RF SQUID

The RF SQUID was invented in 1965 by Robert Jaklevic, John J. Lambe, Arnold Silver, and James Edward Zimmerman at Ford.^[4] It is based on the AC Josephson effect and uses only one Josephson junction. It is less sensitive compared to DC SQUID but is cheaper and easier to manufacture in smaller quantities. The major part of fundamental measurements in biomagnetism even of extremely small signals have been performed, using RF SQUIDS (Tonotopic representation of the auditory cortex by Romani and Williamson 1980, brainstem auditory evoked magnetic field by Erné et al. 1987^[6]). The RF SQUID is inductively coupled to a resonant tank circuit. Depending on the external magnetic field, as the SQUID operates in the resistive mode, the effective inductance of the tank circuit changes, thus changing the resonant frequency of the tank circuit. These frequency measurements can be easily taken, and thus the losses which appear as the voltage across the load resistor in the circuit are a periodic function of the applied magnetic flux with a period of Φ₀. For a precise mathematical description refer to the original paper by Erné et al.^[3]^[7]

The traditional superconducting materials for SQUIDs are pure niobium or a lead alloy with 10% gold or indium, as pure lead is unstable when its temperature is repeatedly changed. To maintain superconductivity, the entire device needs to operate within a few degrees of absolute zero, cooled with liquid helium.

"High temperature" SQUID sensors are more recent; they are made of high temperature superconductors, particularly YBCO, and are cooled by liquid nitrogen which is cheaper and more easily handled than liquid helium. They are less sensitive than conventional "low temperature" SQUIDs but good enough for many applications.

Uses

The extreme sensitivity of SQUIDs makes them ideal for studies in biology. Magnetoencephalography (MEG), for example, uses measurements from an array of SQUIDs to make inferences about neural activity inside brains. Because SQUIDs can operate at acquisition rates much higher than the highest temporal frequency of interest in the signals emitted by the brain (kHz), MEG achieves good temporal resolution. Another area where SQUIDs are used is magnetogastrography, which is concerned with recording the weak magnetic fields of the stomach. A novel application of SQUIDs is the magnetic marker monitoring method, which is used to trace the path of orally applied drugs. In the clinical environment SQUIDs are used in cardiology for magnetic field imaging (MFI), which detects the magnetic field of the heart for diagnosis and risk stratification.

Probably the most common use of SQUIDs is in magnetic property measurement systems (MPMS). These are turn-key systems, made by several manufacturers, that measure the magnetic properties of a material sample. This is typically done over a temperature range from that of 4 K to roughly 190 K, though higher temperatures mean less precision.

For example, SQUIDs are being used as detectors to perform magnetic resonance imaging (MRI). While high field MRI uses precession fields of one to several teslas, SQUID-detected MRI uses measurement fields that lie in the microtesla regime. Since the MRI signal drops off as the square of the magnetic field, a SQUID is used as the detector because of its extreme sensitivity. The SQUID, coupled to a second-order gradiometer and input circuit, along with the application of gradients, are the fundamental entities which allow a research group to retrieve noninvasive images. SQUID-detected MRI has advantages over high field MRI systems, such as the low cost required to build such a system, and its compactness. The principle has been demonstrated by imaging human extremities, and its future application may include tumor screening.

Another application is the scanning SQUID microscope, which uses a SQUID immersed in liquid helium as the probe. The use of SQUIDs in oil prospecting, mineral exploration, earthquake prediction and geothermal energy surveying is becoming more widespread as superconductor technology develops; they are also used as precision movement sensors in a variety of scientific applications, such as the detection of gravitational waves. Four SQUIDs were employed on Gravity Probe B in order to test the limits of the theory of general relativity.

It has also been suggested that they might be implemented in a quantum computer.^[8] These are the only macroscopic devices that have been cited as possible qubits in this context.

References

^ Ran, Shannon K’doah (2004) (PDF). Gravity Probe B: Exploring Einstein's Universe with Gyroscopes. NASA. p. 26. http://einstein.stanford.edu/content/education/GP-B_T-Guide4-2008.pdf.
^ D. Drung, C. Assmann, J. Beyer, A. Kirste, M. Peters, F. Ruede, and Th. Schurig (2007). "Highly sensitive and easy-to-use SQUID sensors". IEEE Transactions on Applied Superconductivity 17 (2): 699. Bibcode 2007ITAS...17..699D. doi:10.1109/TASC.2007.897403. http://ib.ptb.de/de/org/7/75/751/SQUID_Stromsensoren/Drung_ASC06_Preprint.pdf.
^ ^a ^b E. du Trémolet de Lacheisserie, D. Gignoux, and M. Schlenker (editors) (2005). Magnetism: Materials and Applications. 2. Springer.
^ ^a ^b J. Clarke and A. I. Braginski (Eds.) (2004). The SQUID handbook. 1. Wiley-Vch.
^ R. C. Jaklevic, J. Lambe, A. H. Silver, and J. E. Mercereau (1964). "Quantum Interference Effects in Josephson Tunneling". Phys. Rev. Letters 12 (7): 159–160. Bibcode 1964PhRvL..12..159J. doi:10.1103/PhysRevLett.12.159.
^ S.N. Erné, M. Hoke, M. Lütkenhöhner, C. Pantev, H.J. Scheer (1987). "Brainstem auditory evoked magnetic fields in response to stimulation with brief tone pulses". Int. J. Neuroscience 37 (3–4): 115–125. doi:10.3109/00207458708987142.
^ S.N. Erné, H.-D. Hahlbohm, H. Lübbig (1976). "Theory of the RF biased Superconducting Quantum Interference Device for the non hysteretic regime". J. Appl. Phys. 47 (12): 5440–5442. Bibcode 1976JAP....47.5440E. doi:10.1063/1.322574.
^ Quantum coherence with a single Cooper pair, V Bouchiat, D Vion, P Joyez, D Esteve, M H Devoret, 1998 Phys. Scr. 1998 165